Snakes, ärgere dich nicht!

Do you remember these board game collections with 6-10 evergreen games and hundreds of different pawns in the box? It doesn't matter which one you take or how old it is, there's always this one game in there: Snakes & Ladders. I hate it.

It's boring. All you do is throw the dice and follow what the board dictates. It's a game of pure chance; you could flip a coin to win and nothing would change (except less time would have been wasted). Yet, I keep meeting people who hold this game dear. It's fascinating and always a great reminder that your own taste is not shared by everyone. I, however, like to have a sense of control over my games. I expect to be rewarded for spending time to think about what to do next.

A good friend of mine and I found one of these dusty board collections in a hospital's waiting room. As we had hours upon hours to kill we played almost every game in there, although we did actively avoid Snakes & Ladders. After playing Mühle (Nine Men's Morris) for the seventh time we finally yielded and decided to give the S&L board some love.

Bored minds get creative, so we decided to spice it up a bit. We wanted to use the S&L board but mix in the movement mechanics of Mensch, ärgere dich nicht!: 

    - Instead of 1, every player would have 4 pawns.
    - After rolling a d6, the player could choose which pawn to move.
    - Ending on a snake's head would move the pawn down to the tail's end.
    - Ending on a ladder would move it up.
    - Ending on a field with an enemy pawn on it would beat it back to "0".
    - To win, a player has to put all 4 pawns right on the "100"-field.

Honestly, we didn't expect much but total chaos - which was exactly what happened. The first rounds consisted of pawn after pawn being beaten back to the start. It seemed like noone would ever finish this game, until my friend managed to slip one past the "brawl zone" with two high rolls in a row.

With this lead she funneled all her eyes into this pawn. My objective now was to catch it. There was a ladder that could close the gap on "13". To increase my chances I placed all my pawns in front of it and tried to wait until she passed the ladder's top at "46". After she did I prayed to the god of dice and managed to knock her pawn down.

The game went on like this for 40 minutes. We played, yelled and sacrificed our loved ones to the dice gods until she ultimately came out as the winner. While shaking hands, congratulating each other for the great game we realized the shocking truth: We just had fun playing Snakes & Ladders!

But why?

Fun is an elusive, subjective thing and we still don't know what's sure to generate it and how or if it can be measured. We do have, however, a sheer endless list of things most likely to kill it. One of the top entries on this list is predictability. If you could predict a game from start to finish with absolute certainty, there would be no reason to play it.

Games need to be unpredictable.

According to game studies, there are three things able to introduce unpredictability into your games: Chance, player choice and mechanics too complex to process. Different genres use different combinations of these and the weight of any one aspect compared to the others can also vary. While strategy games like chess put their emphasis on player choice and complexity, games of chance value... well, chance - like S&L does.

At the same time, different players have different tastes on what kind of combinations they like or dislike. While some players may enjoy games with chance outshining choice and complexity, my friend and I just don't.

By introducing more pawns and giving the player the choice on which pawn to move, we introduce player choice into the game and devalue chance, thus increasing our fun. For this to work, however, the choice needs to be true - it needs to matter.

Let's check if choice matters in our game. If choice matters, a decision can be measured in it's value, meaning there are good and bad moves (or correct and wrong choices) to make. To simplify the thought process we have to abstract the board. To do this, we sort all fields into three categories: Good, Neutral and Bad - G, N & B:

G-fields are all ladders, an enemy pawn and the "100"-field.
N-fields are those without special function.
B-fields are snakes plus any field an enemy pawn can reach in the next round.

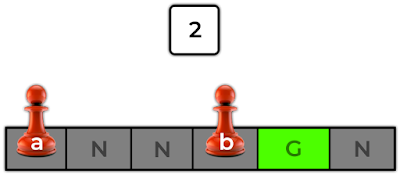
Now, let's say we have the following constellation and roll a "2":

We had a chance of 2/6 to get a G-roll, a dice roll placing us on a G. We needed a "4" for the a-pawn or a "1" for the b-pawn. A "2" is not a good roll, but we can maximize it's value by choosing the correct pawn to move. If we moved the a-pawn, we'd still have a chance of 2/6 on a G-roll next round. If we moved the b-pawn, we'd skip the G-field and reduce our chance of G-rolling next round to 1/6, as only the b-pawn would be able to step on a G-field.

True, this is a very simple situation but it does prove that choice matters. Let's check another constellation for fun - a little more complicated this time. For the sake of visibility I didn't mark enemy pawns and their 6 fields at the front as G- or B-fields:

With that "3" roll we can't move the a-pawn as it'd land on our b-pawn. The b- and c-pawn would both skip a B-field. The chance of getting a G-roll would also neither in- or decrease. Our b- and c-pawn will be in danger no matter which one we move as we can't get out of reach. This would mean both moves are equivalent in value, right?

Wrong. We haven't considered the enemy pawns, especially how it affects their chances to get a G-roll. Currently, Blue holds a chance of 3/6 to get a G-roll the coming round: Stepping on the G-field with a "5" or taking a pawn with "1" or "2". If we move our b-pawn Blue can take it with a "4", if we move the c-pawn Blue can take it with a "5". Blue's G-rolls actually look like this:

    - current: 1,2,5

    - if b-pawn moves: 1,4,5

    - if c-pawn moves: 2,5

If we move our c-pawn and Blue rolls a "5", it has to make a decision on which G-roll to execute: stepping on the field or taking our c-pawn. This means, the chance for Blue to get a G-roll gets decreased to 2/6 (down from 3/6). Choosing the c-pawn is thus the superior move.

Now, imagine introducing multiple G-fields with different values, even more B-fields you should avoid, having 4 pawns to juggle and considering up to 12 enemy pawns on the field. The complexity increases dramatically! If you combine this with chance putting you into one of 6 the power of [number of players] possible situations each round, you get a hugely unpredictable and surprisingly complex strategy game.